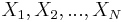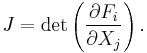Jacobian conjecture
In mathematics, the Jacobian conjecture is a celebrated problem on polynomials in several variables. It was first posed in 1939 by Ott-Heinrich Keller. It was later named and widely publicised by Shreeram Abhyankar, as an example of a question in the area of algebraic geometry that requires little beyond a knowledge of calculus to state.
The Jacobian conjecture is notorious for the large number of attempted proofs that turned out to contain subtle errors. As of 2011, there are no plausible claims to have proved it.
Contents |
Formulation
For fixed N > 1 consider N polynomials Fi for 1 ≤ i ≤ N in the variables
and with coefficients in an algebraically closed field k (in fact, it suffices to assume k=C, the field of complex numbers). We consider these as a single vector-valued function
- F: kN → kN
whose components are the Fi. The Jacobian determinant J of F is by definition the determinant of the N × N matrix consisting of the partial derivatives of Fi with respect to Xj:
J is itself a function of the N variables X1, …, XN; indeed it is a polynomial function.
The condition
- J ≠ 0
enters into the inverse function theorem in multivariable calculus. In fact that condition for smooth functions (and so in particular for polynomials) ensures the existence of a local inverse function to F, at any point where it holds.
Since k is algebraically closed and J is a polynomial, J will be zero for some complex values of X1, …, XN, unless we have the condition
- J is a constant.
Therefore it is a relatively elementary fact that
- if F has an inverse function G:kN → kN, then J is a non-zero constant.
The Jacobian conjecture is a strengthening of the converse: it states that
- if J is a non-zero constant, then F has an inverse function G:kN → kN, and G is regular (in the sense that its components are given by polynomial expressions).
Results
Wang (1980) proved the Jacobian conjecture for polynomials of degree 2, and Bass, Connell & Wright (1982) showed that the general case follows from the special case where the polynomials are of degree 3. Moh (1983) checked the conjecture for polynomials of degree at most 100 in 2 variables.
The Jacobian conjecture is equivalent to the Dixmier conjecture.[1]
See also
Notes
- ^ P.K. Adjamagbo, A. van den Essen, A proof of the equivalence of the Dixmier, Jacobian and Poisson conjectures, Acta Math. Vietnam. 32 (2–3) (2007) 205–214
References
- Bass, Hyman; Connell, Edwin H.; Wright, David (1982), "The Jacobian conjecture: reduction of degree and formal expansion of the inverse", American Mathematical Society. Bulletin. New Series 7 (2): 287–330, doi:10.1090/S0273-0979-1982-15032-7, ISBN 9791982150327, MR663785
- Belov-Kanel, Alexei; Kontsevich, Maxim (2007), "The Jacobian conjecture is stably equivalent to the Dixmier conjecture", Moscow Mathematical Journal 7 (2): 209–218, arXiv:math/0512171, Bibcode 2005math.....12171B, MR2337879
- A. van den Essen (2001), "Jacobian conjecture", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=J/j120010
- Keller, Ott-Heinrich (1939), "Ganze Cremona-Transformationen", Monatshefte für Mathematik und Physik 47 (1): 299–306, doi:10.1007/BF01695502, ISSN 0026-9255, http://dx.doi.org/10.1007/BF01695502
- Moh, T. T. (1983), "On the Jacobian conjecture and the configurations of roots", Journal für die reine und angewandte Mathematik 340: 140–212, ISSN 0075-4102, MR691964 Preprint titled "On the global Jacobian conjecture for polynomials of degree less than 100", http://resolver.sub.uni-goettingen.de/purl?GDZPPN002200376
- A. van den Essen, Polynomial automorphisms and the Jacobian conjecture, ISBN 3-7643-6350-9 (http://emis.mi.ras.ru/journals/SC/1997/2/pdf/smf_sem-cong_2_55-81.pdf).